高频电路不稳定?教你从零实战小功率开关电源
本章节以实用小型电源的设计为例,说明电源设计的方法。控制电路形式为它激式,采用UC3842为PWM控制电路。电源开关频率的选择决定了变换器的特性。开关频率越高,变压器、电感器的体积越小,电路的动态响应也越好。但随着频率的提高,诸如开关损耗、门极驱动损耗、输出整流管的损耗会越来越突出,对磁性材料的选择和参数设计的要求也会越苛刻。另外,高频下线路的寄生参数对线路的影响程度难以预料,整个电路的稳定性、运行特性以及系统的调试会比较困难。在本电源中,选定工作频率为85 kHz。
1
电源设计指标
小型电源输入、 输出参数如下:
输入电压:AC 110/220 V;
输入电压变动范围:90~240 V;
输入频率:50/60 Hz;
输出电压:12 V;
输出电流:2.5 A。
2
电路结构的选择
小功率开关电源可以采用单端反激式或者单端正激式电路,使电源结构简单,工作可靠,成本低。与单端反激式电路相比,单端正激式电路开关电流小,输出纹波小,更容易适应高频化。用电流型PWM控制芯片UC3842构成的单端正激式开关电源的主电路如图6-1所示。
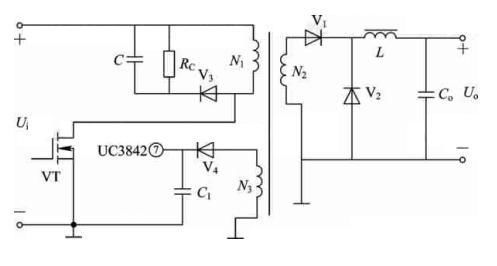
单端正激式开关电源加有磁通复位电路,以释放励磁电路的能量。在图6-1中,开关管VT导通时V1导通,副边线圈N2向负载供电,V4截止,反馈电线圈N3的电流为零;VT关断时V1截止,V4导通,N3经电容C1滤波后向UC3842⑦脚供电,同时原边线圈N1上产生的感应电动势使V3导通并加在RC吸收回路。由于变压器中的磁场能量可通过N3泄放,而不像一般的RC D磁通复位电路消耗在电阻上,因此可达到减少发热,提高效率的目的。
03
元件设计
1)变压器和输出电感的设计
依据UC3842应用方式,选定定时电阻RT=1.8 kΩ,定时电容CT=10μF。确定开关频率f=85 kHz,周期T=11.8 μs。
设计单端控制开关电源时,一般占空比D最大不超过0.5,这里选择D=0.5,则:
根据电源规格、输出功率、开关频率选择PQ26/25磁芯,磁芯截面积S=1.13 cm2,磁路有效长度l=6.4 cm,饱和磁通密度BS=0.4 T。取变压器最大工作磁感应强度Bmax = BS/3≈0.133 T,则电感系数A为:
变压器原边线圈匝数N1为:
式中,Ui为最小直流输入电压。
交流输入电压的最小值约为90 V, Ui=90× ≈127 V,得出N1=49.9匝,取50匝。原边线圈电感L=AN12=11.1 mH。
副边线圈匝数为:
式中,UDF为整流二极管V1上的压降;UL为输出电感L上的压降。
取UDF+UL=0.7 V,代入式(6-4),得N2=10匝。副边线圈电感:
开关管断开时,N1两端将会产生感应电动势,为了保证开关管正常工作,将感应电动势限制到e=300V。反馈电线圈向UC3842提供U=12V的工作电压,按电容C1上的电压UC=16V计算,以保证有足够的供电电压给UC3842。由N3=(UC/e)N1可得N3=2.67匝,取3匝。
变压器副边电流为矩形波,其有效值为:
导线电流密度取4 A/mm2,所需绕组导线截面积为1.77/4≈0.44 mm2。同样可选择原边绕组导线,原边电流有效值为:
所需绕组导线截面积为0.354/4=,选用截面积为0.096 21mm2的导线(?0.41 mm)。取输出电感的电流变化量ΔIL=0.2Io=0.5A,则输出电感为:
式中, U2为副边线圈最小电压。计算得:
取UDF=0.5 V,Uo=3 V,代入式(6-8)可得L=140μH。根据输出电感上的电流IL=Io,所需绕组导线截面积应为2.5/4=0.625 mm2,故选择截面积为0.6362 mm2导线(?0.96 mm)。
2) 开关管、整流二极管和续流二极管的选择
由于开关管断开时原边线圈N1两端的感应电动势限制到eL≈300 V,交流输入电压经全波整流、电容滤波后,直流输入电压的最大值。
所以整流二极管所承受的最高反向电压为:
续流二极管所承受的最高反向电压为:
流过整流二极管和续流二极管的最大电流为:
得ID=2.75 A。根据以上计算选择肖特基半桥MBRCT,平均整流电流为25 A,反向峰值电压为120 V。开关管选用MOSFET 2SK793,漏源击穿电压为900 V,最大漏极电流为3 A。
3)反馈电路的设计
电流反馈电路采用电流互感器,通过检测开关管上的电流作为采样电流,原理如图6-2 所示。电流互感器的输出分为电流瞬时值反馈和电流平均值反馈两路,R2上的电压反映电流瞬时值。开关管上的电流变化会使UR2变化,UR2接入UC3842的保护输入端③脚,当UR2=1 V时,UC3842芯片的输出脉冲将关断。通过调节R1、 R2的分压比可改变开关管的限流值,实现电流瞬时值的逐周期比较,属于限流式保护。输出脉冲关断,实现对电流平均值的保护,属于截流式保护。